在本章中我们学习了概率的定义.下面我们结合概率论发展的历史,对概率的定义做更深入的了解.
概率论是一门研究随机现象的数量规律的学科.它起源于对赌博问题的研究.早在16世纪,意大利学者卡丹与塔塔里亚等人就已从数学角度研究过赌博问题.他们的研究除了赌博外还与当时的人口、保险业等有关,但由于卡丹等人的思想未引起重视,概率概念的要旨也不明确,于是很快被人淡忘了. 一般把1654年作为概率论诞生的一年.这一年中,法国数学家帕斯卡与费马在往来的信函中讨论了诸如赌博中如何合理分配赌金等问题.后来惠更斯也加入研究.他们在研究中涉及了概率论的一些基本概念,如事件、概率、数学期望等.
赌金分配问题:
甲、乙两人同掷一枚硬币.规定:正面朝上,甲得一点;若反面朝上,乙得一点,先积满3点者赢取全部赌金.假定在甲得2点、乙得1点时,赌局由于某种原因中止了,问应该怎样分配赌金才算公平合理.
帕斯卡:若再掷一次,即使乙获胜,也是平分赌金,所以甲至少可拿到一半赌金;若再掷一次,甲胜、乙胜可能性相同,两人平分剩下的一半赌金.故甲应得赌金的3/4,乙得赌金的1/4.
费马:结束赌局至多还要2局,结果为四种等可能情况:
情况 1 2 3 4
胜者 甲甲 甲乙 乙甲 乙乙
前3种情况,甲获全部赌金,仅第四种情况,乙获全部赌注.所以甲分得赌金的3/4,乙得赌金的1/4.
帕斯卡与费马用各自不同的方法解决了这个问题.虽然他们在解答中没有明确定义概率的概念,但是,他们定义了使某赌徒取胜的机率,也就是赢得情况数与所有可能情况数的比,这实际上就是概率,所以概率的发展被认为是从帕斯卡与费马开始的.
在概率论发展早期,人们研究最多的是等可能概型,即我们本章中学习的古典概型.其中概率的定义
 ,
,
法国数学家拉普拉斯在1812年把它作为概率的一般定义,这就是概率的古典定义.在概率论发展早期这个定义解决了相当多的概率问题,因而得到广泛使用.比如下面著名的问题
德·梅尔问题
一颗骰子投4次至少得到一个六点与两颗骰子投24次至少得到一个双六,这两件事那个更容易遇到?
概率的古典定义,易得
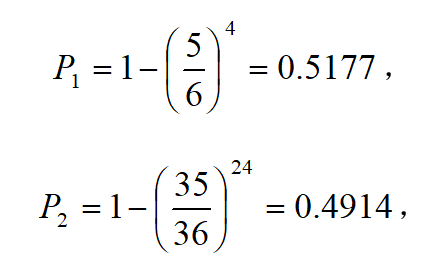
所以前者发生概率超过1/2,更容易遇到.
这个问题之所以著名,因为它是德·梅尔向帕斯卡提出的问题之一,正是这些问题导致帕斯卡与费马的著名通信.
但是,不是古典概型问题,概率该如何定义呢?许多人坚信,只要找到适当等可能描述,就可以给概率问题以唯一的解答.但事实并非如此,如著名的贝特朗奇论:
贝特朗奇论
在单位圆内随机地取一条弦,问它的长度超过该圆内接等边三角形的边长(即√3)的概率是多少?
这是几何概率问题,但对“随机地”理解不同,采用不同的等可能假设,则会得到大相径庭的答案.举例如下:
解法( 一) 弦长只与它到圆心的距离有关.而与方向无关.不妨假设它垂直于某条直径,假定弦的中点在直径上均匀地分布,那么随机地取一条弦,只有它到圆心的距离小于1/2时,其长才会大于√3,故所求概率为1/2.
解法(二) 任何弦交圆周两点,假设端点在圆周上均匀的分布,先固定其中一个端点,以此点为顶点做一个等边三角形.那么随机地取一条弦,只有它落入此三角形中,其长才会大于√3,这样的弦的另一端所在的弧长为圆周的1/3,故所求概率为1/3.
解法( 三) 弦被其中点唯一决定.假设弦的中点在圆内均匀地分布,那么随机地取一条弦,只有当它的中点落在半径为1/2的同心圆内时,其长才会大于√3,而小圆面积为单位圆面积的1/4,故所求概率为1/4.
以上三种答案对于各自的随机试验而言都是正确的.因此,使用诸如“随机地”、“等可能”、“均匀地”,一般要指明具体含义.
由于采用等可能定义概率有困难,所以后来定义概率时只是明确概率应该具有的基本性质,这样对不同的随机试验可以给出相应的概率.这样就有了用频率来定义概率.这就得到概率的统计定义.在历史上,第一个对当试验次数n逐渐增大,频率稳定在其概率上这一论断给以严格的意义和数学证明的是早期概率论史上最重要的数学家之一雅各布·伯努利.在第五章我们将学习伯努利大数定律.这里要指出的是,概率论中的伯努利并不是一个人,而是一个家族,这就是数学界传为美谈的伯努利家族,这个家族出了许多数学家,在数学的很多分支都有所建树,留下大量诸如伯努利试验,伯努利定理,伯努利定律等等.概率论的第一本专著是1713年问世的雅各布·伯努利的《推测术》.
在概率问题早期的研究中,逐步建立了事件、概率和随机变量等重要概念以及它们的基本性质.后来由于许多社会问题和工程技术问题,如:人口统计、保险理论、天文观测、误差理论、产品检验和质量控制等.这些问题的提法,均促进了概率论的发展,从17世纪到19世纪,伯努利、隶莫弗、拉普拉斯、高斯、泊松、切贝谢夫、马尔可夫等著名数学家都对概率论的发展做出了杰出的贡献.在这段时间里,概率论的发展简直到了使人着迷的程度.但是,随着概率论中各个领域获得大量成果,以及概率论在其他基础学科和工程技术上的应用,由拉普拉斯给出的概率定义的局限性很快便暴露了出来,甚至无法适用于一般的随机现象.因此可以说,到20世纪初,概率论的一些基本概念,诸如概率等尚没有确切的定义,概率论作为一个数学分支,缺乏严格的理论基础.
上述问题直到19世纪末才得到较好地解决,当时数学界盛行公理化潮流,即把最基本的假设公理化,其他的结论则有公理导出来.在这种背景下,1933年,前苏联数学家柯尔莫哥洛夫发表了著名的《概率论的基本概念》,提出了概率论公理化结构,明确定义了概率的基本概念,从此概率论成为严谨的数学分支,得到迅速发展.现在公理化的概率定义得到广泛的认同.
但关于概率的争论并没有结束.我们学习了条件概率与贝叶斯公式,设随机试验的样本空间为S,B为其事件, A1,A2,…,An为S的一个划分,且
P(B)>0,P(Ai)>0(i=1,2,…,n)
则
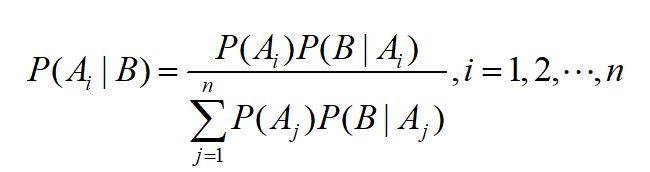
在这里,不妨设事件B表示某人生病,A1,A2,…,An是导致生病的诸多原因,则称P(Ai)为先验概率,它表示各种原因发生的可能性的大小,一般由以往的经验或资料给出;称P(Ai|B)为后验概率,它的意义是,既然试验结果导致事件B发生,那么这个信息有助于我们重新认识导致各种原因发生的可能性的大小.医生进行诊断要做的就是从各种原因中找出最可能的,从而对症下药.一般称这种利用贝叶斯公式进行的推断为贝叶斯推断,在统计中有大量应用.一般来讲,后验概率P(Ai|B)的大小受到先验概率P(Ai|)的影响.那么先验概率的选取就很重要了.如果先验概率是以大量的实际调查资料给出,符合概率的频率解释,没有任何问题;但如果先验概率是以主观形式给出的,比如对物价、汇率变化的估计,对某种形势的人为的判断,最有代表性的莫过于对宇宙中有没有UFO等的判断,这种概率就是主观概率,贝叶斯学派采用这种主观概率.这种把概率解释为主观信仰的做法引起了很大争议.由此,在做统计推断时,贝叶斯推断与我们第七、八章要学习统计推断在原理上是完全不同的.
对于贝叶斯概率解释,考虑如下的这些情况:
(1) 你有一个装了白球和黑球的盒子,但是不知道它们的数量;
(2) 你有一个盒子,你从中取了n个球,一半黑,一半白;
(3) 你有一个盒子,你知道有同样数量的黑球和白球;
求下一个取出的球是黑球的概率.
贝叶斯概率对于所有三种情况答案居然都是0.5.
这里涉及到贝叶斯学派会事先主观选取不同的分布模型,不做详细论述了.感兴趣的读者可自行查阅相关资料.关于主观概率的争论仍在进行中.