美国数学家伯格米尼曾经做过一个别开生面的试验:在一个世界杯足球赛场上,他随机地在某号看台上召唤了22个球迷,请他们分别写下自己的生日,结果竟发现其中两人同生日. 怎么会这么凑巧呢?下面我们通过计算机模拟伯格米尼试验.
用22个1~365的可重复随机整数来模拟试验结果
(1) 产生22个1~365的可重复随机整数,若其中出现两个或两个以上的重复整数时,就认为这22个人中有生日相同的人,否则就认为没有生日相同的人;
(2) 重复(1)1000次,统计出现生日相同的频数和频率并填入下表;
(3) 产生40个,50个,64个随机数,重复(1)(2),并且与生日相同的概率值进行比较.
输入下面的Matlab语句,进行模拟试验.
clear all
n=22;
xh=1000;
fre=0;
for i=1:xh
s=0;
a=fix(unifrnd(1,366,1,n));
b=unique(a);
[rb,cb]=size(b);
if cb<n
fre=fre+1;
end
end
fre % 输出生日相同的频数
fre/xh % 输出生日相同的频率
事实上,设随机选取r人,A={至少由两人同生日},则
 ,
,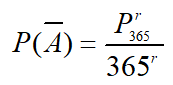 ,所以有
,所以有
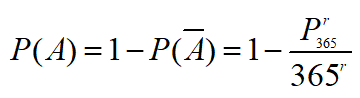
我们可以计算出当r=22,40,50,64的生日相同的概率值分别为0.476,0.891,0.970,0.997.
通过计算机模拟实验,请同学比较出现生日相同的频率与概率,你们能得到什么结论?
|
n=1000 |
r |
|||
|
r=22 |
r=40 |
r=50 |
r=64 |
|
|
出现生日相同次数 |
|
|
|
|
|
出现生日相同频率 |
|
|
|
|
|
出现生日相同概率 |
0.476 |
0.891 |
0.970 |
0.997 |