本章开始讨论的是多维随机变量.从数学哲学的角度上讲,从一维随机变量到二维随机变量,发生的是质的变化,我们要做到的是抓住它们之间的联系与区别.联系是多方面的,比如学习随机变量,首先考虑分布函数是什么,其次对于离散型随机变量,考虑分布律;对于连续性随机变量,考虑概率密度函数,考虑分布函数与概率密度函数之间的关系.这条线对于不论是一维还是多维随机变量都是一样的.而区别也是明显的.二维随机变量作为一个整体,具有作为个体的两个一维随机变量所不具备的整体性质.而且这两个一维随机变量之间的关系也错综复杂.作为概率论中最重要的概念之一,随机变量的独立性在概率论中占有举足轻重的地位.由于从二维到三维乃至n维随机变量发生仅仅是量的变化,所以我们一般
仅就两个随机变量的独立性问题加以讨论,三维以上可以类推.
独立性是概率论中独有的一个概念.这个概念的引入对概率论的发展影响巨大.概率论的很多理论基本上都在独立性的假定下建立发展起来的.近代开始才有了对不独立的概率模型的研究,但一般还需假定具有某种微弱的独立性.关于这点,在今后的学习中会有越来越深的体会.学习独立性时,重要的是会使用独立性,而不是判别独立性.
作为概率论中非常重要的一个问题,若干个独立服从同类型分布的随机变量之和还是一个随机变量,它会具有哪些性质呢?首先讨论的当然还是它的分布函数.如果它仍然服从原来的分布,则称这个分布具有再生性或者可加性.下面我们介绍一些具有再生性的分布.
(一)正态分布
设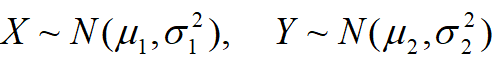 且X、Y相互独立,Z=X+Y仍服从正态分布且有
且X、Y相互独立,Z=X+Y仍服从正态分布且有
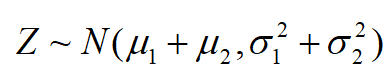 .
.
推广到n个独立正态随机变量之和的情况,即若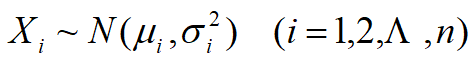 ,且它们相互独立,则Z=X1+X2+Λ+xn仍然服从正态分布,且
,且它们相互独立,则Z=X1+X2+Λ+xn仍然服从正态分布,且
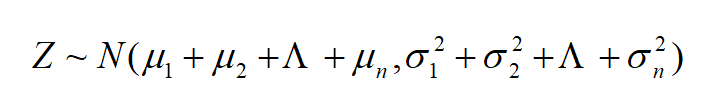
更一般地,可以证明有限个相互独立的正态随机变量的线性组合仍然服从正态分布.
(二)二项分布
设X~B(n,p),Y~B(m,p)且X、Y相互独立,Z=X+Y仍服从二项分布且有
Z~B(n+m,p)
(三)泊松分布
设X~P(λ1),Y~P(λ2)且X、Y相互独立,Z=X+Y仍服从泊松分布且有
Z~P(λ1+λ2)
二项分布与泊松分布的可加性可以直接证明,建议读者作为练习.
(四)伽马分布
随机变量X具有密度函数
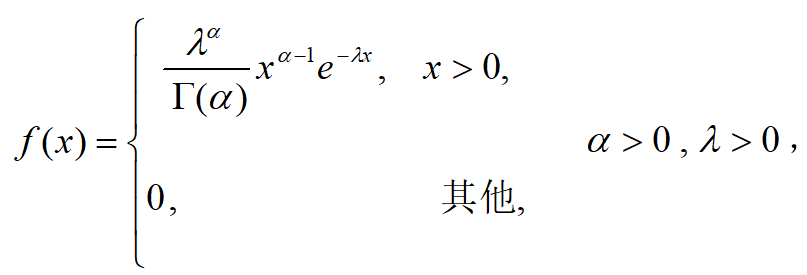
称X服从参数为α,λ的Г分布.记为X~Г(α,λ).其中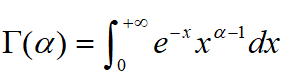 是所谓的Г函数,满足Г(1)=1,Г(n+1)=n!,Г(t+1)=tГ(t),(t>0).
是所谓的Г函数,满足Г(1)=1,Г(n+1)=n!,Г(t+1)=tГ(t),(t>0).
设X~Г(α,λ),Y~Г(β,λ)且X、Y相互独立,Z=X+Y仍服从Г分布且有
Z~Г(α+β,λ)
作为伽马分布的特例,许多其他的分布也有再生性.如下面的
(五)卡方分布
当X~Г(α,λ)时,令α=n/2,λ=1/2,则随机变量X具有密度函数
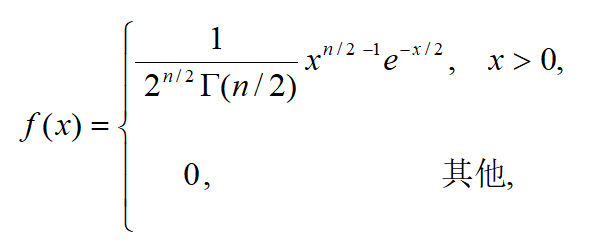
此时称X服从自由度为n的X 2分布.记为X~ X 2(n).
设X~ X 2(n),Y~ X 2(m)且X、Y相互独立,Z=X+Y仍服从X 2分布且有
Z~ X 2(n+m)
(五)指数分布
当X~Г(α,λ),显然当α=1时,X就服从参数为λ的指数分布.也就是说,指数分布是伽马分布的特例,相当于X~Г(1,λ).虽然指数分布不具有可加性,但在伽马分布这个意义下,也可以讲指数分布具有可加性.
设X~Г(1,λ),Y~Г(1,λ)且X、Y相互独立,Z=X+Y仍服从Г分布且有
Z~ Г(2+λ)
教材中还讲过指数分布的一个性质,重复一下,n个相互独立同分布的指数分布,其最小值的分布还服从指数分布,参数为其参数的n倍.