2-6 独立随机变量之和的分布

设X，Y相互独立，都服从（0,1）上的均匀分布，求Z=X+Y的概率密度.首先，利用卷积公式可求得Z=X+Y的密度函数如下：

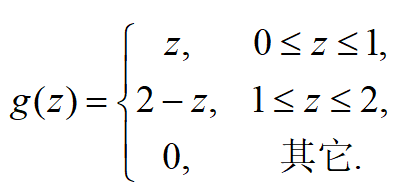
下面用模拟方法来模拟它的概率密度：

(1)  产生两组服从（0,1）上均匀分布的相互独立的随机数x_i，y_i，i=1,1,2,∧,n，令n=1000. 计算z_i=x_i+y_i；

(2)  用数据z_i作频率直方图，并利用卷积公式求得的密度函数在同一坐标系内画出图形作比较. 

(注：在利用密度函数画图时，可令高为g(z)·Δz·n ，其中Δz为画直方图时选择的区间长度，请考虑一下这是为什么？)

输入以下的Matlab语句，可以实现这个模拟过程. 令n=1000，10000重复上述试验，并得出你结论.

clear all

n=1000;

x3=0:0.1:2;

x=unifrnd(0,1,1,n);

y=unifrnd(0,1,1,n);

z=(x+y);

hist(z,x3)

h = findobj(gca,'Type','patch');

set(h,'FaceColor','r','EdgeColor','w')

x1=0:0.01:1;

gz1=x1;

x2=1:0.01:2;

gz2=2-x2;

hold on

plot(x1,gz1*(n*0.1),'-k')

hold on

plot(x2,gz2*(n*0.1),'-k')