箱中装有大小、形状相同的10个球,三个标有号码0,三个标有号码1,两个标有号码2,两个标有号码3. 从箱中任取一球,记下号码后再放回箱中为一次试验.记X为所得号码,则X是随机变量,其概率分布为:
|
X |
0 |
1 |
2 |
3 |
|
pk |
0.3 |
0.3 |
0.2 |
0.2 |
(1) 进行N=100次试验,统计试验中取得0号球、1号球、2号球、3号球的次数N0,N1,N2,N3,算出N次试验所得号码的平均值
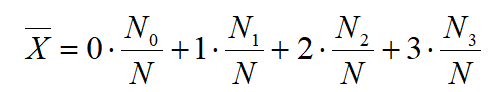
并与数学期望
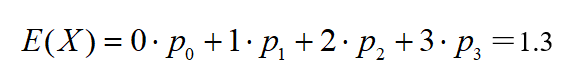
作比较.
(2)分别取N=50,200,2000,5000重复实验1,观察N的取值对 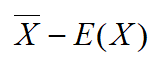 的影响.
的影响.
结论:每组试验结果均在数学期望1.3附近波动,一般来说,随着N增大, 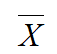 越来越稳定在E(X)附近.
越来越稳定在E(X)附近.
练习1:自行选定参数,分别绘出二项分布、泊松分布,均匀分布、指数分布、正态分布的概率分布曲线或概率密度曲线,观察数学期望对应曲线上的点. 你发现了什么?
练习2:轰炸效果问题.
假设有100个目标需要摧毁,模拟飞机轰炸,每次随机地击中一个目标,且必击中一个目标(可以重复地击中). 计算摧毁全部100个目标平均所需的飞机次数,并进行模拟(用1~100可以重复的随机整数模拟试验结果),输入下面的Matlab语句,完成模拟实验.
实验1中练习2轰炸效果的matlab语句.
clear all
for i=1:10000
n(i)=0;
pd=zeros(1,100);
while sum(pd)<100
z=randperm(100);
pd(z(1))=1;
n(i)=n(i)+1;
end
end
m=mean(n) %输出全部摧毁100个目标平均所需的飞机次数
实验2的matlab语句
clear all
mu=3;sig1=1;sig2=2;a=1;n=2000 %输入参数及有关的值
x1=mu-4*sig2:0.01:mu+4*sig2;
y1=normpdf(x1,mu,sig1);
plot(x1,y1) %随机变量X的概率密度图形
hold on
y2=normpdf(x1,mu,sig2);
plot(x1,y2,'r') %随机变量Y的概率密度图形
px1=normcdf(mu+a,mu,sig1)-normcdf(mu-a,mu,sig1) %P(X–μ|>a)
px2=normcdf(mu+2*a,mu,sig1)-normcdf(mu-2*a,mu,sig1) %P(X–μ|>2a)
py1=normcdf(mu+a,mu,sig2)-normcdf(mu-a,mu,sig2) % P(|Y–μ|>a)
py2=normcdf(mu+2*a,mu,sig2)-normcdf(mu-2*a,mu,sig2) % P(|Y–μ|>2a)
xr=normrnd(mu,sig1,1,n);
yr=normrnd(mu,sig2,1,n);
qj1=[mu-a,mu+a];
qj2=[mu-2*a,mu+2*a];
fx1=histc(xr,qj1);
fx2=histc(xr,qj2);
fy1=histc(yr,qj1);
fy2=histc(yr,qj2);
frex1=fx1(1)/n %随机数X落入到区间[μ-a,μ+a]内的频率
frex2=fx2(1)/n %随机数X落入到区间[μ-2a,μ+2a]内的频率
frey1=fy1(1)/n %随机数Y落入到区间[μ-a,μ+a]内的频率
frey2=fy2(1)/n %随机数Y落入到区间[μ-2a,μ+2a]内的频率