设X,Y都是连续型随机变量，均服从正态分布：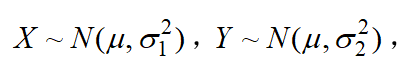
其中σ1<σ2，输入后面的Matlab语句，完成以下实验.
(1) 画出两个分布的概率密度图形；
(2) 取N=2000，分别产生服从两个分布的二组随机数，并画直方图；
任选常数a>0（注意大小适中），计算P(|X-μ|>a)，P(|X-μ|>2a)，P(|Y-μ|>a)，P(|Y-μ|>2a)，同时统计两组随机数落入到区间[μ-a,μ+a]和[μ-2a,μ+2a]内和区间外的频率.
通过以上的实验，你会得到什么结论？
练习3 设X~P(2)，Y~P(20)，分别产生两组随机数，完成类似上面的实验，观察参数对随机数取值的影响，并解释原因.
练习4 设X服从参数为2的指数分布，Y服从参数为1的指数分布，分别产生两组随机数，观察参数对随机数取值的影响，并解释原因.
实验２的matlab语句
clear all
mu=3;sig1=1;sig2=2;a=1;n=2000 %输入参数及有关的值
x1=mu-4*sig2:0.01:mu+4*sig2;
y1=normpdf(x1,mu,sig1);
plot(x1,y1) %随机变量X的概率密度图形
hold on
y2=normpdf(x1,mu,sig2);
plot(x1,y2,'r') %随机变量Y的概率密度图形
px1=normcdf(mu+a,mu,sig1)-normcdf(mu-a,mu,sig1) %P(X–μ|>a)
px2=normcdf(mu+2*a,mu,sig1)-normcdf(mu-2*a,mu,sig1) %P(X–μ|>2a)
py1=normcdf(mu+a,mu,sig2)-normcdf(mu-a,mu,sig2) % P(|Y–μ|>a)
py2=normcdf(mu+2*a,mu,sig2)-normcdf(mu-2*a,mu,sig2) %P(|Y–μ|>2a)
xr=normrnd(mu,sig1,1,n);
yr=normrnd(mu,sig2,1,n);
qj1=[mu-a,mu+a];
qj2=[mu-2*a,mu+2*a];
fx1=histc(xr,qj1);
fx2=histc(xr,qj2);
fy1=histc(yr,qj1);
fy2=histc(yr,qj2);
frex1=fx1(1)/n %随机数X落入到区间[μ-a,μ+a]内的频率
frex2=fx2(1)/n %随机数X落入到区间[μ-2a,μ+2a]内的频率
frey1=fy1(1)/n %随机数Y落入到区间[μ-a,μ+a]内的频率
frey2=fy2(1)/n %随机数Y落入到区间[μ-2a,μ+2a]内的频率