本章中我们学习了一些常见的重要的概率分布.一个概率分布是否重要主要取决于以下几点:(1)分布是否应用广泛;(2)分布是否具有良好的理论性质;(3)分布是否具有一定的延展性,即是否可以导出其他的分布.下面我们要介绍的分布满足以上所有条件或其中几条.
(一) 概率论中最重要的分布—正态分布
正态分布无疑是我们必须掌握的分布,它是概率论与数理统计中最重要的分布,不是之一.这些在本章中已有详尽论述.这里不再赘述.正态分布又称为高斯分布.在概率论发展历史上,误差分析是概率论的重要生长点之一,19世纪初德国数学家高斯(Gauss)在研究测量误差是引进了正态分布并发展了有广泛应用的最小二乘法(至今这仍是概率论与实际生产有广泛联系的领域之一),从此,进入了正态分布在概率统计中占统治地位的时代,此时同时流行的还有拉普拉斯的中心极限定理.为纪念高斯在对正态分布的研究方面的贡献,人们把正态分布又称为高斯分布(虽然早在高斯之前,拉普拉斯和隶莫弗已经把正态分布引入概率论中了).正态分布将伴随我们本书学习的始终.
(二) 几个基于同一概率模型的分布
伯努利概型是一种非常重要的概率模型,它是概率论历史上最早研究的模型之一,同时也是得到最多研究的模型之一.它是讨论在相同条件下可以重复进行试验的数学模型.在多重伯努利试验中,设每次试验成功的概率为p,失败的概率为q=1-p,考察以下随机变量服从的分布:
(1)X表示直到首次试验成功为止的试验次数,则X服从参数为p的几何分布.其分布律为
P(X=k)=pqk-1,k=1,2, Λ
几何分布给出了等待某个事件A发生时,所等待的次数为k的概率,作为一种等待分布,几何分布应用也很广泛.而且它具有一个非常独特的性质—无记忆性.假设在前m次试验中都未成功,我们用Y表示直到首次试验成功为止的试验次数,则
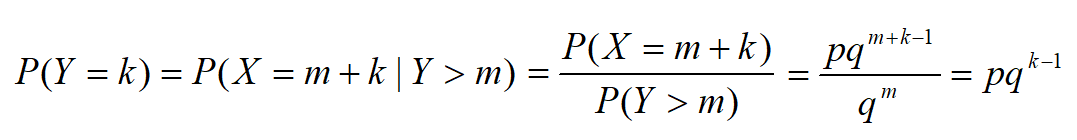
也就是说,此时Y仍然服从参数为p的几何分布,这就好像是说,它已经忘记了前面已经失败了m次.或者说,直到首次试验成功为止的试验次数与前面已经失败次数无关.在离散型分布中,只有几何分布具有这种无记忆性.
(2)X表示直到r次试验成功为止的试验次数,则X服从参数为r、p的帕斯卡分布或负二项分布.其分布律为
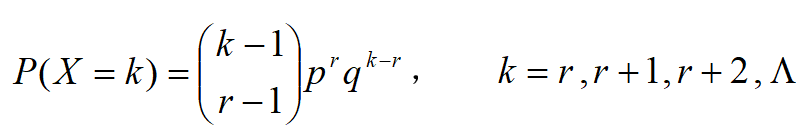
显然,r=1时,就是上面的几何分布.负二项分布与几何分布的关系类似于二项分布与两点分布的关系.现在,负二项分布的研究在逐步深入当中.这里举一个可应用负二项分布的著名的问题:
巴拿赫火柴盒问题:
有一个人左右两个衣袋中各装一盒火柴,每盒火柴都是N根,当他吸烟时,随机地取出一盒划着一根,求他的其中一盒火柴用完同时另一盒火柴正好剩下M根的概率.(答案见本文最后)
(3)X表示n次试验中成功的试验的次数,则X服从参数为n、p的二项分布.其分布律为我们熟知的
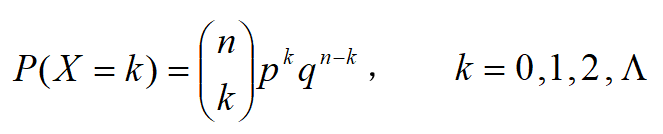
当k=1就是两点分布.两点分布又称为伯努利分布.
描述n重伯努利试验中某个事件发生的次数的随机变量就服从二项分布.二项分布是离散型分布中非常重要的一种,尤其在抽样检查中被广泛使用.它的计算相对麻烦,往往需要进行近似计算.
(三)应用广泛的泊松分布
泊松分布是由法国数学家泊松于1837年作为二项分布的近似引入的.近年来,人们对这种分布的重要性的认识与日俱增.已经发现许多许多的随机现象服从泊松分布.主要集中在两个领域:一是社会服务性领域,如电话交换台收到的呼叫次数、车站到来的乘客人数都近似服从泊松分布,因此,运筹学和管理学中泊松分布占优重要地位;二是物理科学中,诸如热电子的发射、放射性物质发射的粒子数等也都服从泊松分布.
还有一个有趣的现象就是许多与“灾难”相联系的现象也与泊松分布相联系.诸如某城市一天中发生的火灾数、发生的交通事故数、一天内邮递遗失的信件数、某医院一天内的急诊病人数、我们这本书中一页中的印刷错误数等等都服从泊松分布.因此,有人称泊松分布是“不吉利”的分布.
(四)“永远年轻”的指数分布
很多与寿命有关的随机现象服从的是指数分布.诸如电子元件的寿命、动物的寿命、随机服务系统中的服务时间、电话问题中的通话时间等等都假定服从指数分布.所以,在排队论和可靠性理论中应用很多.与几何分布一样,指数分布也具有所谓的无记忆性,设随机变量X服从参数为λ的指数分布,∀ s,t >0,有
P(X > s+t | X >s)=P(X > t )
仿照几何分布的做法很容易得到这个结论,读者可以作为练习自己完成.如果把X解释为寿命,上式说明,如果已知某人的年龄为s,那么他再活t年的概率与年龄s无关.所以人们开玩笑地称指数分布是永远年轻的.
需要指出的是,各种教材中所用的指数分布有不同的表达.有的书中这样定义指数分布:
随机变量X具有密度函数
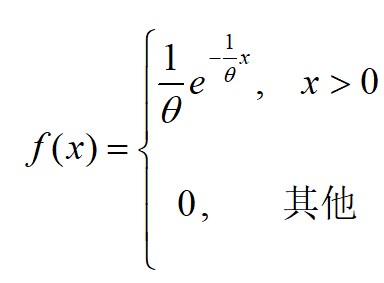 ,
,
称X服从参数为θ的指数分布.
有的书中也把指数分布称为负指数分布.
(五)奇妙的[0,1]区间上的均匀分布
作为[a,b]区间上的均匀分布,我们已知它具有独特的“均匀”的性质:随机变量落在其中任何一个区间上的概率只与区间长度有关,而与位置无关.所以,X~U[0,1],则有
P(X≤x)=x
但是考虑过这样的问题吗?假设X是随机变量,分布函数为F(x)(这里F(x)连续),将X带入分布函数中,令ξ=F(X),则可以证明ξ还是随机变量.那么,ξ服从什么分布呢?答案是,ξ在[0,1]区间上服从均匀分布.这是因为F(X)是不降函数,对任意0≤y≤1,可以定义
F-1(y)=inf{x:F(x)>y}
作为F(x)的反函数,这里,inf表示集合的下确界(最大的下界).则对0≤x≤1,有
P(ξ≤x)= P(F(X)≤x)= P(X≤F-1(x))= F(F-1(x))= x
由均匀分布的性质可知ξ=F(X)服从[0,1]区间上的均匀分布.这里,我们再次看到分布函数法的重要应用.
反之,ξ在[0,1]区间上服从均匀分布,对任意,分布函数F(x),令
X= F-1(ξ)
则
P(X≤x)= P(F-1(ξ)≤x)= P(ξ≤F(x))= F(x)
因此X的分布函数就是F(x).
这样,我们只要能产生[0,1]区间上服从均匀分布的随机变量的观察值,就能通过变换X=F-1(ξ)产生分布函数为F(x)的随机变量的观察值.一般的做法是用数学的方法产生[0,1]区间上服从均匀分布的随机变量的观察值,称为均匀分布随机数,再利用变换X=F-1(ξ)得到任意分布F(x)的随机数.这种思想在蒙特卡洛方法中有重要应用.
概率论以及后面的数理统计中还有许多具有特殊性质的分布,我们在后面的章节中从不同的角度再做介绍.
巴拿赫火柴盒问题解答:这里p=1/2,不妨设右边盒空而左边剩M根,应该右边盒摸过N+1次,前N次用掉N根火柴,第N+1次发现没火柴了;左面盒硬应摸过N–M次.所以根据帕斯卡分布,用X表示直到N+1次试验成功为止的试验次数,有
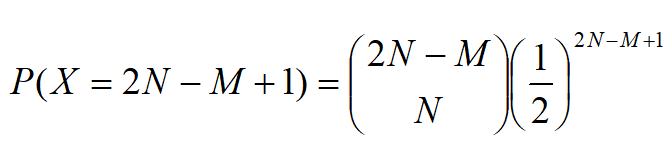 ,
,
同样,也可能出现左边盒空而右边剩M根,概率相同,所以,所求概率为
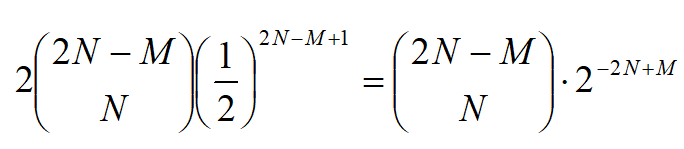 .
.